Compound Expressions
And, Or, Not
In Python, a compound Boolean expression combines multiple Boolean values or expressions using logical operators. The three logical operators used in Python are “and”, “or”, and “not”.
The “and” operator returns True if both the expressions on either side of the operator are True. Otherwise, it returns False. In other words, the whole expression is true only if each individual part of the expression is true. Consider the example below:
if temperature > 70 and weather == "sunny":
print("Go to the beach 🏖️")
In the above example, the compound expression will only be true if the temperature is greater than 70 and the weather is sunny; if either one of these individual expressions is false, the whole expression becomes false.
The “or” operator returns True if at least one of the expressions on either side of the operator is True. Otherwise, it returns False. In other words, the whole expression is true if just one individual part of the expression is true. Consider the example below:
if temperature < 50 or weather == "rainy":
print("It's not nice outside, you should stay in")
In the above example, the compound expression will be true if the temperature is less than 50 or the weather is rainy; if only one of these individual expressions is true, it makes the whole expression false. For instance, if the temperature is 80 degrees but the weather is rainy, the expression would be true because one part of it is true.
The “not” operator is a unary operator that returns the opposite of the Boolean value of the expression it precedes. For example, not True would evaluate to False, while not False would evaluate to True. Consider the example below:
rainy = False
if not rainy:
print("Play Ball!")
else:
print("Rain delay")
The following table may help make sense of the outcomes of various compound Boolean expressions:
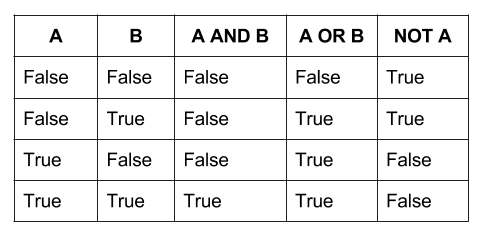
Keep in mind that we can combine as many Boolean expressions as we like, and they will still follow the same logic. For instance, A and B and C and D and E requires all five expressions to be true in order to make the entire expression true. F or G or H requires just one of the three expressions to be true to make the entire expression true.
Precedence of Logical Operators
When you mix the logical operators in an expression, Python will evaluate them in order, which is called the operator precedence. The not operator, then the and operator, then the or operator will be evaluated in order when they all exist in a compound expression.
Based on these precedences, Python will group the operands for the operator with the highest precedence first, then group the operands for the operator with the lower precedence, and so on.
In case an expression has several logical operators with the same precedence, Python will evaluate them from the left to right:

Replit Practice
Updated Order of Operations
Factoring in these new logical and comparison operators, we evaluate expressions according to the following precedent:
- Parentheses: ( )
- Exponents: **
- Multiplication, Division, Modulus: *, /, //, %
- Addition, Subtraction: +, –
- Comparison: ==, !=, >, >=, <, <=
- Logical not
- Logical and
- Logical or
There are a few additional operators that exist within Python that go beyond the scope of this exam, but you can read about here: https://www.programiz.com/python-programming/precedence-associativity
